Coordinates in the Sky, from Flat Earth Academy

HOME > > FLAT EARTH ACADEMY HOME > > ASTRONOMY HOMEPAGE > > FINDING STUFF (in sky, in general)

Coordinates In The Sky

(Sub-page below "Finding Stuff in the Sky")

(filename: linesforsky.htm)

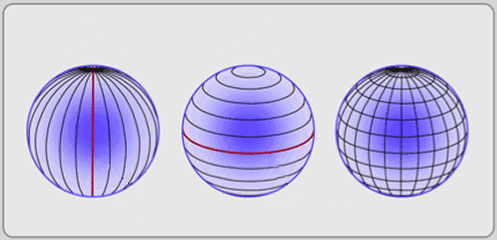
(The image above was adapted from one at https://giscommons.org/earth-and-map-preprocessing/, a page with lots of Interesting Stuff.)

Flat Earth Academy offers a more general page about finding stuff in the sky over your head. This page concentrates on the system which has been designed to establish coordinates in the sky overhead. The system "marks numbered lines" among the stars, like we have "marked" the earth with latitude and longitude "lines", so that we can say where things are.

If we were saying where something was on the earth...

If you wanted to tell someone where Paris is, you could say, "Start at London", go 210 miles roughly southeast, and you will be there. If you could specify the direction of travel with a compass heading, your instructions would be better. Knowledge is power.

Of course, to tell someone how to find Paris that way, you both have to know where London is.

On the Flat Earth Academy page about finding constellations, we use something like the "starting from London..." approach.

Another way to send someone to Paris is to say "Go to longitude 2.3° East, latitude 48.9° North. Of course, you both need to know the "lat/long" system, but the benefit is that you no longer need to know where London is.

The basic idea of specifying points on a sphere is simple: You draw two sets of lines (the "lat" lines, and the "long" lines) on the sphere, give them numbers, and to specify a particular point you just say which latitude and longitude lines cross where the point is.

"Lat/ Long" for the heavens.

Here you will be introduced to a rigorous scheme for saying "where" something is in the sky. A scheme useful for astronomy. What would that be good for? With it, you can find anything in the sky. Suppose you've heard that the Horsehead Nebula is interesting? Wikipedia will tell you that you can find it at "right ascension 05h 40m 59.0s, declination -02° 27' 30.0"... and when you've finished this page, you should be able to point your telescope towards it, if you are inclined to do so. Or suppose a new comet is headed towards the earth, and is still too faint to find just by looking at the sky in general. Someone will have published "where to look" in terms of right ascension and declination.

Elsewhere, I have recommended that you think of "everything" that interests stargazers and astronomers as follows. The scale is all wrong to represent reality... but it works well for most other needs. (I've done a page on the true scale of things.)

Imagine that the sun is a ball 400cm in diameter. And let's imagine the earth a ball 1cm in diameter, orbiting 5m from the sun. (Those numbers are "all wrong", by the way. The differences are much greater... but those numbers are fine for what I want.

Now add to your imaginary picture of the universe a huge hollow brass ball 200m in diameter. With lots of glowing LEDs stuck onto the inside surface. And our "sun" and "earth" (and the other planets of the solar system) floating and moving inside the huge ball, at its center.

The glowing LEDs stuck to the inside of the huge sphere are the stars (and galaxies, etc).

Think of the sphere as being still, with earth spinning 'round, once a day, and going around the sun once a year.

The positions of the stars, relative to one another do not change.

The model works pretty well, if you can imagine yourself on the spinning, orbiting earth. (It may help to imagine yourself as an ant! You have to imagine yourself small, so that when you are "on" the earth, it is so "big" that it blocks your view of parts of the field of stars.)

The most strained part of the analogy is as follows: When you are on the side of the earth facing the sun, you can't see the stars. You only see the stars when you are on the side of the earth facing away from the sun.

If you can get your head around that, then you should see that which stars you see (at night) change as the earth trundles around its orbit.

Remember: we're working towards a system of lines with numbers, rather like the latitude, longitude lines used on earth to say, for instance, where Paris is.

We will get there! Deep breath; keep reading.

Our great sphere, the one that holds all the stars, is an example of a "celestial sphere" (WP). You might almost call it "the" celestial sphere, it is so useful. (Of you leave out the sun and its planets, and don't ever imagine yourself outside of our solar system, there is, more or less, only one celestial sphere.

Now, over the inside surface of the sphere, among the LEDs, imagine painting two sets of "lines". (Arcs, if you want to be strictly accurate in your use of terms. "Lines" running along the curved surface.)

The first all start at the point directly "above" the earth's north pole, as defined by the axis of the earth's rotation. "True" north, vs. magnetic north.) They fan out, being quite wide apart halfway "down" the sphere, and then all come together again at the point directly "below" the earth's south pole.

In other words, they are similar to earth's latitude lines.

If you do one every 15°, you get 24 such lines.

Latitudes are given in degrees, of course. The lines we're talking about here are "numbered" in hours, for the following reason:

If there were no sun, what someone lying on their back, on the equator, looking staight up (as that person feels his the local gravity) would see would repeat after 24 hours.

Here's what I mean by that, in case it isn't clear.

Imagine being the beam of a light-house. As you swing around, first you point at one thing, then you point at another. But what you see at different parts of the rotation repeats itself over and over again.

A person, lying on their back as described above, would see the same things over and over again, because what they are lying on is rotating. (Even though it is a bit bigger than the lamp of the lighthouse!)

Moving on...

Forgetting for the moment any stars NOT at some point directly overhead, you could give a number to the stars you are looking at particular points in the cycle by deciding on a start point ("zero"), and saying how many hours past "zero" you waited to get to the stars you want to give a number to.

The start point: I can't easily point you to where "zero" is on the stars' sphere, but the middle star in Orion's Belt is at very nearly "5 hours". An hour after that star is overhead someone on the equator, the star 15° to the left (as you look out into space, if you are facing south) will be overhead. (If you are south of the equator, you may well be looking north at the heavens, and if so, it will be the star 15° to the right of the one that was overhead an hour ago.)

(I've explained how to find Orion's Belt in the page about some basic constellations and how to find them without knowing about the numbers the page you are on introduces.)

I'm cheating slightly here. The middle star of Orion's Belt will be "straight ahead" to someone lying on their back, on the equator, at the right time. At least as far a "left and right" is concerned, if the viewer' head is north of his/her feet.

At different seasons, the star will be somewhat above or below "directly overhead", in terms of the "up and down", i.e. "north and south", of things.

Sigh. NOT as bad as it seems, but you have to keep the different bits straight in your head. (The problems all stem from the fact that the axis of the earth's rotation is not perpendicular to the plane of the earth's orbit.)

But! We have our first set of lines. If I tell you that the middle star of Orion's Belt (Alnilam) is at "5 hours", I am telling you its "right ascension" (WP). (Good news: there is no "left ascension" to worry about!)

Further good news: The other lines set of lines we need, to say "where" something is in the heavens, are what you probably imagine them to be. They are very like the earth's lines of latitude, although in the heavens they are called lines of "declination" (WP).

The "first" line of declination, analgous to earth's equator, is drawn around the inside of the sphere along the place half-way between the two points where all the lines of right ascension come together. As with the earth's the equator, the galactic grid's equator is line number "zero".

I hope it will reinforce several things I'm trying to show you if I mention that the "zero" line for declination shares one plane with the earth's equator.

The declination for the middle star of Orion's Belt (Alnilam) is nearly zero. (Earlier, I told you that Alnilam's right ascension was about 5 hours, so now you have everything you need to find Alnilam without reference to anything else, as long as you can "find" the lines of right ascension and of declination. (We'll come to that "finding" later)).

For declination=0, the declination line will be at right angles to all of the lines of right ascension.

Imagine yourself on the earth, looking out at the sphere with the stars, with your arm outstretched, pointing your finger to where declination equals zero. Move your finger "up". (I.e. away from declination=0 at right angles to it.) When you have raised your finger 10°, you are pointing at declination=10°. All of "declination=10°" is parallel to the "declination=0" line, aka the galactic grid's equator. From certain points of view, you will see lines of declination curving, and not curving the same amount. But in reality, all of the "rings" of declination are parallel to one another. (The lines of right ascension are not parallel to one another.)

Lines of declination on the sphere with the stars are like lines of latitude on the earth. (They're the ones which run east and west.)

Just to be thorough: I've already explained that if you go up from declination=0 ten degrees, you reach declination=10°. If you go down ten degrees, you reach -10°. ("Negative 10 degrees.")

The declination of objects right at the top or bottom of the sphere are at declination 90°, or negative 90°, respectively. (Again, just as with latitude coordinates.

Why bother? Declination, Right Ascension?

Back at the start, I told you that they give you a very direct way to locate things in the sky.

"All" you need is some kind of "instrument".

You could make one!

It will be a bit like one of the big guns on a battleship's bow. It can swing left and right ("traverse"), and the barrel can go up and down. ("elevate").

For an alternative analogy for what our instrument needs, imagine, if you know them, a pan- and- tilt CCTV or IP cam. Pan and tilt mountings have a base plate. On it there is a platform which rotates ("pan"). And on the rotating platform, the camera is on somethat allows the operator to tilt the camera up and down. That's just what we need for our "find a given right ascension/ declination" device! It would only need the camera to be replaced with a pointer, or something like the sights of a rifle. Of course, if the pan-tilt mechanism were sufficiently robust, you could simply mount your telescope directly on that. And people do have exactly that sort of thing on their telescopes... but "sufficiently robust" (and stable) translates to "very expensive". Sigh.

A naval gun's mounting is always horizontal, and that of an IP cam is usually horizontal. For our "find things in heaven" instrument that will be okay... if we are at the north or south pole... but only then.

Instead of a gun barrel, our device will carry a pointer. It will move left and right. (As in the gun traversing) and it will go up and down. (As in the gun elevating.)

Here's the first tricky bit: The plane of the pointer's "traverse" axis needs to be parallel with the axis of the earth. Mechanically, that's a little tricky to arrange, but as long as you know...

Where North is
What your latitude is

... then you can set your instrument up correctly.

The good news is that marking your instrument for declination is easy. I hope I don't need to explain that?

Now we come to right ascension. This is easier, mechanically, but calibrating the instrument is trickier.

It is trickier because the earth is spinning. You can set your instrument up at midnight, and adjust the right ascension scale so that if the pointer is pointing, say, at right ascension 4 hours, 26 minutes, then that's the reading on the scale. If you then leave it alone, it won't still be pointing at 4:26 a short time later, but with a simple instrument, it will still say that the pointer is pointed at 4:26. (We won't go into making an instrument with a right ascension scale that moves itself.)

Remember: The line for "4:26" runs up and down the "star sphere" in a fixed place. If you were looking that way at midnight, and didn't move a muscle for five minutes, the earth turning beneath your feet would now have you looking somewhere else. That's why your instrument "goes wrong" within moments, and seriously wrong in tens of minutes, however carefully you first set it up.

So here's what I propose for your instrument: You need a disk which spins, mounted beneath the arm holding the pointer. The "holding" (of the pointer, by the arm) should allow the pointer to go up and down. Any "left and right" should be accomplished by the "arm holding" being mounted so that it rotates, always staying at right angles to the plane of the right ascension scale.

On the underlying "table" that the device "sits" on, there should be a reference mark, placed thus:

Before trying to find something in the heavens with the instrument, set the elevation of the pointer to the required declination. That should be "locked in", so that the elevation of the pointer doesn't change.

Rotate the disc with right ascensions on it so that the current time lines up with the reference mark. Now swing the pointer- on- its- arm left and right, until it is pointing towards the required line of right ascension. Remember... if you don't find what you were looking for quickly, you will have to adjust the disc (relative to the reference mark) again, to allow for the earth's spinning.

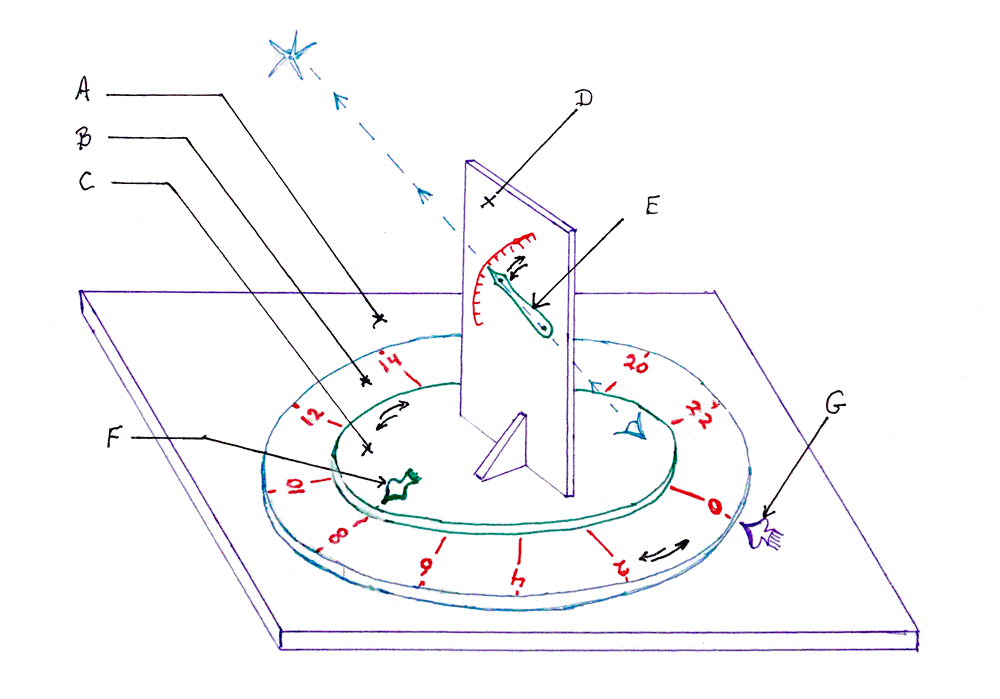
A: The base of the instrument. Mounts to a fixed "post" (or tripod) of some kind, which is inclined to the local "horizontal" by an amount depending upon the latitude of the place the instrument is located. The plane of this base must be parallel to the plane of the earth's equator, or, to put it another way, perpendicular to the axis of the earth's rotation.

B: On the base, a large disc, which can be rotated.

C: On top of the first disc, a second disc, which can also, and independently, be rotated. The share a common center.

D: Firmly fixed to the upper disc, a perpendicular board, with....

E: An "arm" which can swing up and down, and which carries some sort of sighting device... "gunsights", perhaps... for "aiming" the pointer at specific places or objects in the sky. (Diagram shows, in cyan, an eye sighting towards a star.)

F: The upper (smaller) rotating disc has an "index pointer" painted on it. In the illustration, it is pointing at the 8, which is painted on the lower (larger) disc. If just the upper disc is rotated a little clockwise, the pointer would then be pointing at the 10.

G: The base also has an index pointer painted on it. In the illustration, it points to the zero. If the lower disc were rotated slightly clockwise, the base's pointer would be pointing at the 22.

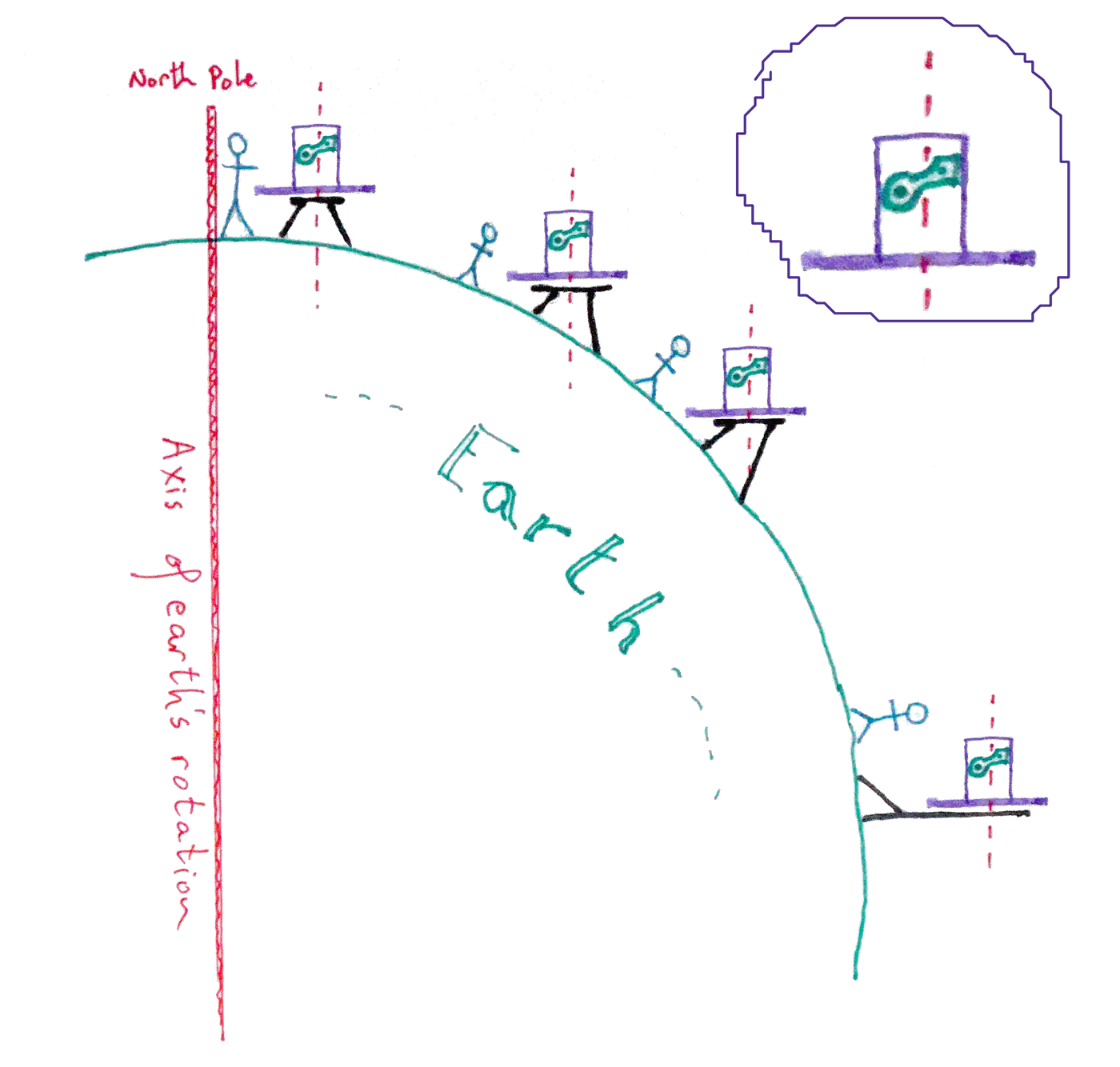
I hope the above goes some way to clarify how the instrument must be mounted, for use? At upper right is an enlarged view of our instrument, copied, as you can see, at the various observing stations.

Think about how this diagram would look in a version for the southern hemisphere!