One approach to making maps is based on measuring angles.
The "proper" instrument for this is the theodolite... but a plane table is simpler to make and use... if a bit cumbersome, and even though it gives answers which have to be converted to degrees... if you need that. (You can just copy the angles off of the result. Or even draw your map directly, as you go along!) (You can make your own theodolite, on almost any budget!)
Before we get to the plane table, a word about the sort of angles we want to measure.
Imagine yourself standing on a hill. In front of you, about 3 miles away there's a church spire, due south of you. And to the southeast, there's a large chimney, part of a factory complex.
If you point to the spire with your right hand, arm extended, and to the chimney with your left hand, arm extended, an angle is formed between your two arms.
One type of map making depends entirely on this sort of angle. Lots and lots of angles like this, for even a modest map. (The link will take you to an activity for hobbyists, schools... and also to illustrations which may clear up what sort of angles we want to measure, if that's not yet clear.)
Note the spelling of "plane". Here we are using it in the sense of "flat".
And "table" is used in the sense of "kitchen table"
If, on the hill-top, you had a kitchen table, you could use that as a plane table.
(A piece of cardboard, with a sheet of paper taped to it, suitably supported, would be more typical... but think "kitchen table" (with a cork surface) for now.
You also have three sturdy straight pins with you.
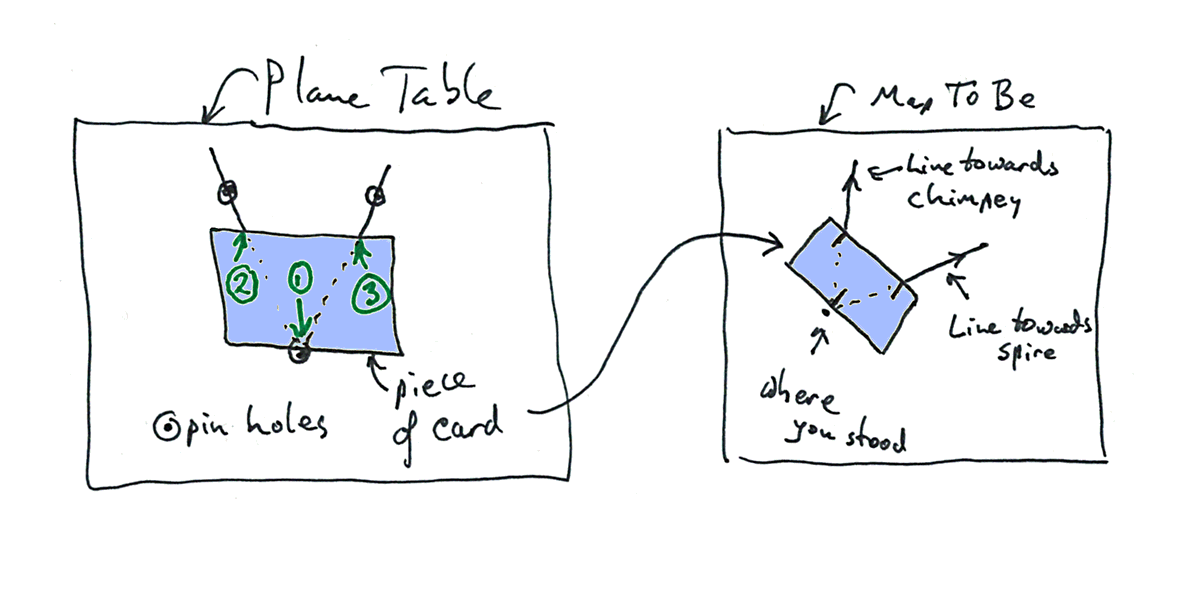
Stick one into the table (or piece of cardboard), with the pin standing vertically, and with most of it above the table. Stick it into the table near you. This is pin "A" in the second diagram.
Now crouch down, and, with your eye, line up that pin with the factory chimney. (Flag "C" in the diagram.) Without moving your head, stick a second pin into the table, this time as far from you as you can reach, with the two pins lined up with each other and with the factory chimney. This is pin "B" in the diagram.
Good! Halfway done!!
In the following, in place of the chimney and spire, I have small triangular flags on poles. Sorry!

Now move your head until the first pin, "A", the one near you, is lined up with the spire (Flag "E".)
And stick another pin (pin "D") into the table, as far from yourself as you can make it, but on the eye- to- first-pin- to- spire line....
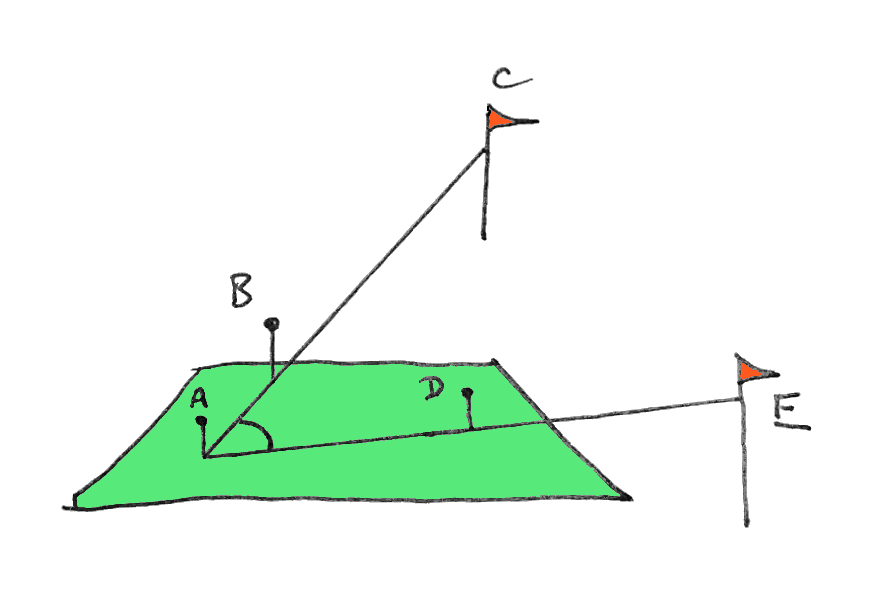
Great! Now you have a board with three pins in it.
If you draw lines between them, you will draw an angle that is the size of the angle you would have had between your arms, earlier, when you were pointing at the two distant objects... the angle you wanted
But you can measure the angle (the one a math teacher would call "CAE") from the two lines defined by the three pins more easily, can't you? And more accurately!
That's how you use a plane table to measure the angle "between" two objects in the distance. Or, more mathematically rigorously, the angle between the two lines passing through your observation point and the objects in the distance.
With such angles, you can make maps... as explained HERE.
Fancier instruments exist... but they only do the same thing... but rather better. The fancier instruments are called theodolites. You can buy an antique one for a few hundred dollars, or a fancy, high precision one for... practically whatever you want to spend. Or you can make your own theodolite!
So far, so good. We have points marked on the plane table which define one or more angles. But "how big" are those angles, in degrees??
Do you need to know? If you are making a map with them you can just "copy" the angles, using a bit of card...

The first answer was rather crude. And useless if you are using a computer program that needs an angle measured in degrees, to draw the map. (Such things can be CREATED, by hobbyists... and there's probably one out there already. Let me know, if you can recommend a free one that runs on, sigh, Windows.)
"All" you need to do to get good angles out of a plane table is...
Start with a large sheet of paper... the larger the better. Your measurements will be more accurate. Or is that "precise"? Or both? (These are important concepts which you should be clear about. The nice folks at labwrite.ncsu.edu have explained precision and accuracy well. (Four short paragraphs!))
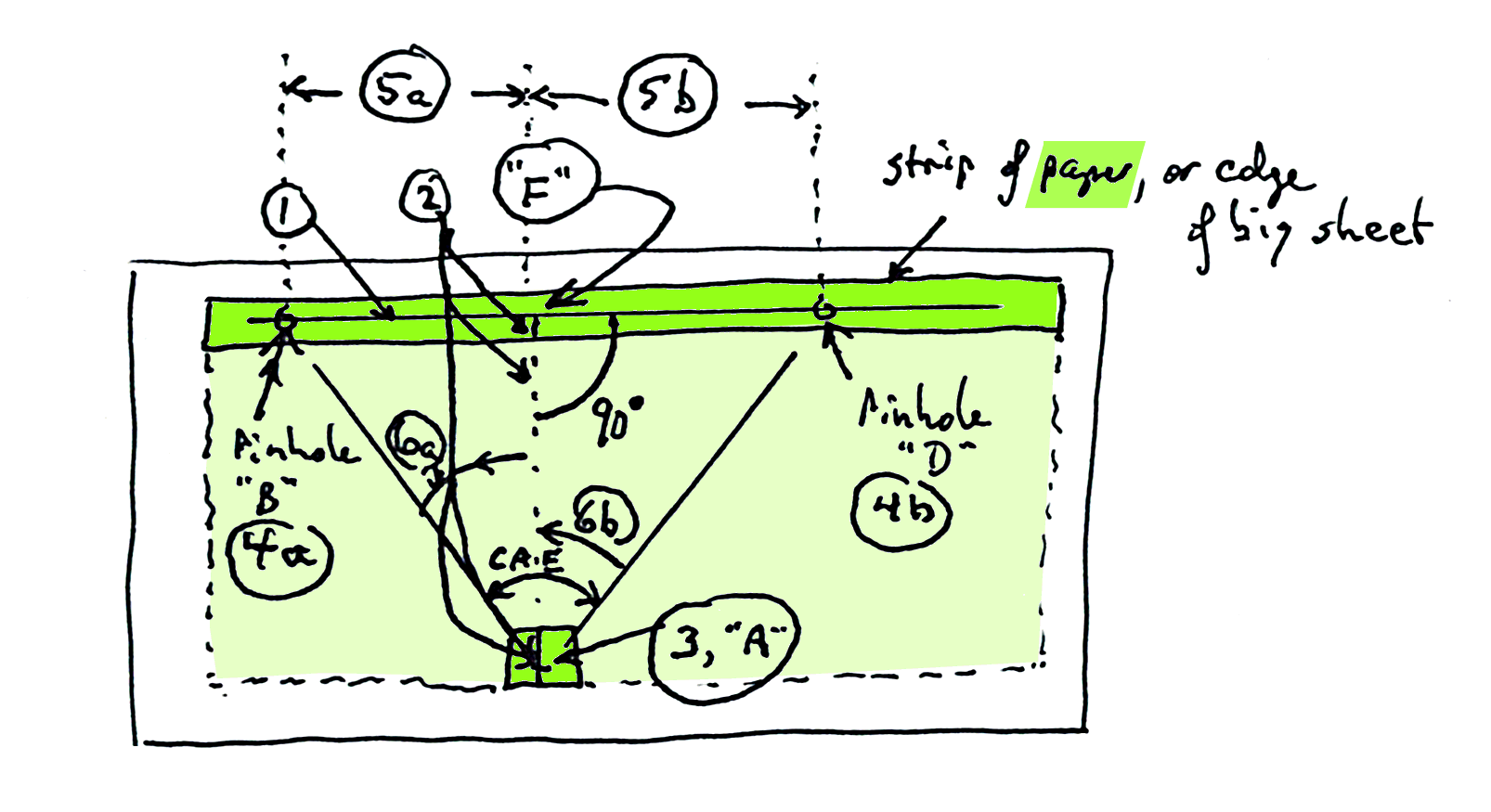
(You CAN make do with a strip of paper, and a smaller piece, if you tape them securely to the table, so they can't move relative to one another. I've shown that in the diagram, with a dotted line standing for the large sheet.) (Diagram below... Yes, it got over-full... just take it slowly... maybe draw what's being explained on a piece of scrap paper.)
1) Draw a line along the edge of the paper which will be farthest from the apex of the angle...
2) "Construct a perpendicular" from about the middle of the line you drew. In other words, draw a line away from it at a right angle, i.e. 90 degrees.
3) Mark a spot somewhere on that perpendicular. This will be the apex of all your angles. (Point "A", using the names we've used elsewhere on this page.)
4) Do an angle.
5) Measure how far B and D are from where the two lines you drew meet, "F".
6) With those two numbers, and the distance from A to F, you can calculate the size of the two angles shown. Add those numbers, and you know CAE!
The calculation isn't as hard as it seems, and could easily be done by a tiny program in a computer. If someone writes it in Lazarus, and will share the sourcecode, let me know and I will publish it here, or provide a link to your page.
Search across all my sites with the Google search button at the top of the page the link will take you to.
Or...
Search just this site without using forms,
Or... again to search just this site, use...
The search engine merely looks for the words you type, so....
*! Spell them properly !*
Don't bother with "How do I get rich?" That will merely return pages with "how", "do", "I", "get" and "rich".
I have other sites. My Google custom search button will include things from them....
One of my SheepdogGuides pages.
My site at Arunet.
This page's editor, Tom Boyd, will be pleased if you get in touch by email.
![]() Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes.
Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes.