I went to a school on a hilltop. An inspirational teacher had a tradition going- each year, the 15 year olds measured the distance from our science building to a flagpole a little over a mile away, on the next hilltop, across a valley.
Not only was it a useful bit of science, but it was fun to be participating in something bigger than "this week's homework". When the year's results were in, the number we'd come up with was compared with the results from previous years.
In the following, I will set out three possible measuring challenges. All are similar to "real world" science, as practiced before the days of satellite images and GPS. All have lessons about how science works. All have safeguards against "clever" teenagers using cheats to work the problems backwards.
The three challenges are...
In each case, you can run the competition for individuals, or for small teams of individuals. In the following, I will say "participants", but you can treat that as "teams" if you wish.
I won't apologize for introducing an element of competition into my proposals. I believe that if competition is properly managed, it can bring out the best in people, make something "interesting", but still not be too harmful to those who "fail".
Having your efforts measured by impersonal, objective, based in reality numbers can give a reward to those who complete a task more successfully, and be a wake-up call for those who have not executed the challenge with craftsmanship.
The "How Far?" challenge is most like the one I remember from my youth. The participants are invited to determine the distance to something too far away to be measured to with tape measures.
The distance will be measured by triangulation, the basis of all large scale maps for over a century, up to about the 1960's.
The basic technique is explained on my mapping by triangulation page.
And here's how the challenge can be run with protection against anyone working the problem backwards. You may have to "tweak" the following, depending on the circumstances you are working in.
First, of course, you need to choose a distant object which is likely to be available, and visible from where your participants will be working, for years to come.
You also need a "baseline" with, preferably, a view to the distant object from each end. The baseline wants to be as long as you can manage, but you need to be able to see each end from the other, and, for teachers, etc, intending to launch this challenge, supervision of your pupils will be a factor.
And a second, nearer, object "put on your map" would be very helpful. I would suggest changing the second object each year. It could be an "unimportant", "randomly chosen" point, marked with stake bearing a small flag to help make it visible.
If what you have to work with makes it possible, something like the following would be ideal...
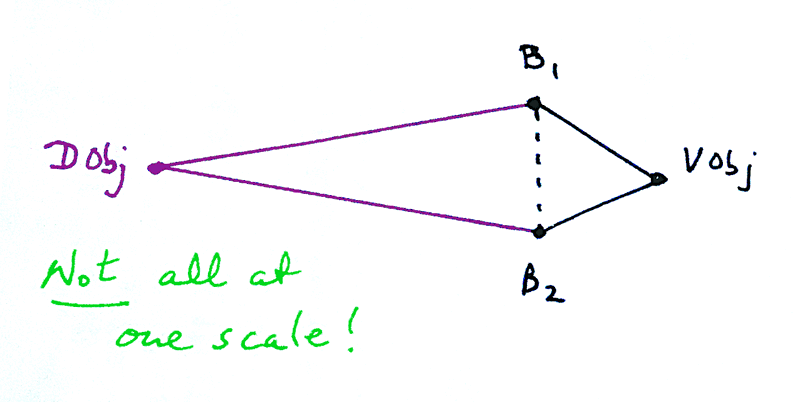
In that, we have the distant object ("DObj") at the left, perhaps a mile from the site where the participants will work.
The rest of the diagram is to a different scale...
"B1" to "B2" is the "baseline" for the mapping. Where they are, if you can manage it, remains the same from year to year. (Baselines are explained elsewhere in detail, and to some extent further down the page.)
"VObj" is the Object which is Varied from year to year.
The participants are given the opportunity of measuring the various angles, and the length of the baseline. If the time available for this is limited, you can give the participants the length of the baseline, or measuring that can be a separate annual challenge- see below.
They are asked to prepare a map, and from the map determine the lengths of B1-VObj and B2-VObj.
The results of the different teams are plotted on a graph by the challenge organizer, and from that, "success" can be evaluated. (The graph is done by the organizer so that results aren't fudged to "fit in" with what others are reporting. It also gives the organizer the opportunity of keeping the least successful participants anonymous, though they will know who they were.)
The results for B1-DObj are also plotted. It isn't "fireproof", but if a participant obtained a "good" answer for where VObj was, it is credible that their answer for where DObj is may actually have been measured, not "worked backwards" from some alternative source of the information.
Another guard against the cheats being able to look better than the honest participants, is to give the participants a figure for the length of the baseline. A slightly wrong figure. In a good year, no one will give you the actual distance instead of the "correct wrong" answer.
After the results are in, explain what you did, tell them the factor needed to change the answer they got to the right answer. Or perhaps do a "measure the actual length of the baseline" as an additional challenge. (See "How long?", below.)
And that's the "How Far" challenge.
Having got "How Far" under our belts, the "How High" challenge is easier to describe.
In this challenge, the participants are invited to determine the height of a flagpole, high building, whatever... something which is going to be there from year to year. Some "significant" item in the local landscape. If you happen to be near a dramatic hill, you might consider measuring the height of that... above some fixed feature near it's base, visible from where the participants will be working... although this adds a few "issues" to the challenge.
The technique is essentially the same as that use din the "how far" challenge.
You measure an angle, do some arithmetic. The angle, in this case, is that which would be between your arms if you extended them fully, and pointed one at the top of the object, and the other at the bottom.
You combine that angle with the angle you get with similar "pointing" at the ends of something like a baseline... a line defined by two points, two points you can directly measure the distance between.
The correspondence between the "how far?" and "how high?" methods may not be immediately obvious. For some participants, one or the other may be more intuitive. Pick the challenge that you feel you can "sell" most successfully... or maybe to both, so that one activity reinforces the learning experienced in the other?
Again, each year, the challenge might also involve measuring the height of something that is re-measured each year, and the height of something that changes each year... to guard against the same thing we were guarding against previously.
You can make maps by triangulation without ever troubling to include a measured baseline. You just won't know the scale of your map.
For me, the "angles" part is the "magic", "fun" part. Measuring a baseline isn't, to me, as much fun. But as a challenge for a group of participants, and as an exploration of an essential element of the old technique for mapping, maybe it has a place.
I would invite all the participants to measure a baseline which could be measured year after year. The participants would submit their results "secretly", i.e. without pre-sharing. When all of the results were in, a graph could be produced, and discussed for the many lessons which could be learned from it.
The story of Roy's baseline across Hampstead Heath could be raised. (I was disgusted that I could get no response from a school with a large playing field on that line, despite writing the headmaster and the head of geography. I was proposing funding an annual prize for a competition measuring a part of "the" baseline.)
This time, to protect the honest from the cheats, I would propose putting a mark somewhere along the baseline... somewhere different each year... and using the participants measurement to that mark as a guide to whether they were actually doing the measurement.
If you had many participants doing the challenge, you could kill several birds with a few stones, as follows...
Here's your baseline, in a crude "diagram"...
Add two or three intermediate "points" to that "line"...
B1----X-------Y------Z-------B2
Now you can have one different groups of participants measure different segments of the whole. There will be no "right answer" to shoot for. (An answer possibly available from someone who did the challenge in a prior year.)
And when the results are in for B1-X, X-Y, Y-Z and Z-B2, they can be combined for an answer to "How Long is B1-B2?".
Furthermore, with several groups of participants each doing a part of the whole measurement, the task is less daunting, if your baseline is long.
I mentioned the Hampstead Heath baseline.
In the late 1700s, the British set about doing a "proper" map of the country.
William Roy oversaw the project. As a part of that, the distance between two points on some more or less open, more or less flat ground about 15 miles WSW of London was measured.
That baseline was about 5 miles long. It was re-measured in modern times, and the original measurement was vindicated... depending on where you look on the internet, you will be told that the new measurement agreed with the old to within less than three feet.... or to within less than 5 inches. Let's go with the measurements being within 3 feet of one another. Three feet in 27,404. Not bad. If someone owed you $270, would you be bothered about 3 cents?
And here's a thought: Let's say that in the late 1700s, Roy drove a stake into the ground at each end of his baseline, to say "These are the ends". Would those stakes still be there, today, so that the re- measuring could re-measure the same distance? Still in the same place, to within inches? I don't think so! But Roy (or at least someone shortly after him) was brighter than that, and looked ahead to the day when someone might want to re-measure. And he took steps. What would you have done to mark two spots in a way that would last hundreds of years? They were still there, as of 2015, at least. (I've seen one of the marks, and "I read it on the internet" that the other is still there, too.)
The Wikipedia article on Roy has information you may appreciate.
Speaking of "still in the same place": Now that we have GPS, a little problem has arisen. There's a channel used by big ships in Australia which is moving. If steps weren't taken to keep the maps up to date, a captain sailing his ship where the channel was previously, would run aground. I'm not talking about the age-old problem of sandbars moving around. This is a channel dug into more permanent geology. But the plate that channel is in is moving... enough to matter!
And lastly, in respect of "moving": When pilots land airplanes, it is really, really good if the plane is traveling in the same direction as the runway. If it is a "north/south" runway, it isn't good if the airplane is flying "east/west".
Runways are named according to the right magnetic compass bearing for landing on that runway. One of the runways in downtown Washington, DC is called "19" because you need to be flying a heading of about 190 degrees. Not long ago, the name of that runway was 18! (Or was it 17?... one or the other)
Did "they" move the runway???
No. Where magnetic north has changed, very slightly. Once upon a time, you had to fly 184 to land on that runway. Now you have to fly 186. (Or logically equivalent numbers.)
Is nothing ever simple? I wish "they" would leave my cheese where I left it!
Search across all my sites with the Google search button at the top of the page the link will take you to.
Or...
Search just this site without using forms,
Or... again to search just this site, use...
The search engine merely looks for the words you type, so....
*! Spell them properly !*
Don't bother with "How do I get rich?" That will merely return pages with "how", "do", "I", "get" and "rich".
I have other sites. My Google custom search button will include things from them....
One of my SheepdogGuides pages.
My site at Arunet.
This page's editor, Tom Boyd, will be pleased if you get in touch by email.
![]() Page q-WILL BE tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes. There were two "unknown attributes" in Google+ button code. Sigh.
Page q-WILL BE tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes. There were two "unknown attributes" in Google+ button code. Sigh.