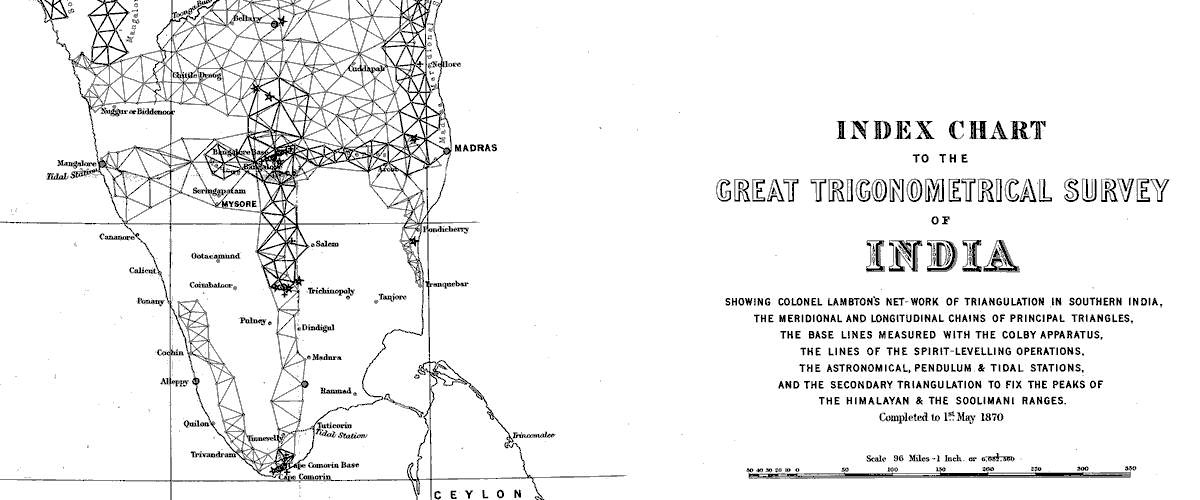
In the 1800s, the British completed a vast project to map many, many, many, points in India. A feat that I suspect will be "special" for a long time to come: The work done, and the logistics involved are extraordinary. The project was, to quote a sentence from Simon Garfield's very readable book, On the Map, about the fascination of maps in general, "the Great Trigonometrical Survey of India- conceived in 1799, commenced in 1802, but only officially titled in 1818."
As a small part of that, they drew the first accurate maps of portions of the Himalayas. Just determining the latitude and longitude of each peak was an impressive feat... but the team also figured out the heights of the different peaks. (They did this by using angles... tiny angles, measured to amazing degrees of precision. You may have come to this page from one or another of my pages on the web about making maps by using angles.)
The team was the first to measure Everest's height. They published their result in 1856.
Due to political constraints at that time, they could not get closer than 108 miles. They could see it... and a number of tall neighbors, though, and set about measuring the heights. At the time, no one knew that Chomolungma, the local name for it, was the highest. From over 100 miles away, how do you distinguish a distant tall mountain from a closer, not- quite- so- high, mountain? (My thanks, by the way, to On the Map for reminding me that I've wanted to write this up for some time, and for some of the accurate facts and figures in this... though I suspect errors made by me remain.)
The surveyors could see the peak from six different locations... locations which they were in the process of locating precisely, as a part of the broader Survey. They took many, many readings of their view of Everest (and neighbors) and averaged them... and came up with a height of 29,000 feet. Thinking the number implausibly "perfect", they added two feet, and reported that Everest was 29,002 feet high. They determined that from measurements taken from between 108 and 118 miles away.
On The Map credits the Bengali mathematician Radhadanth Sikdar with doing the arithmetic. (You really don't want to try to understand all of that... At these levels of precision, the curve of the earth has to be factored in... And that's just one of the "details".)
Andrew Waugh was in charge of the Great Trigonometrical Survey of India at the time the follooing was produced...
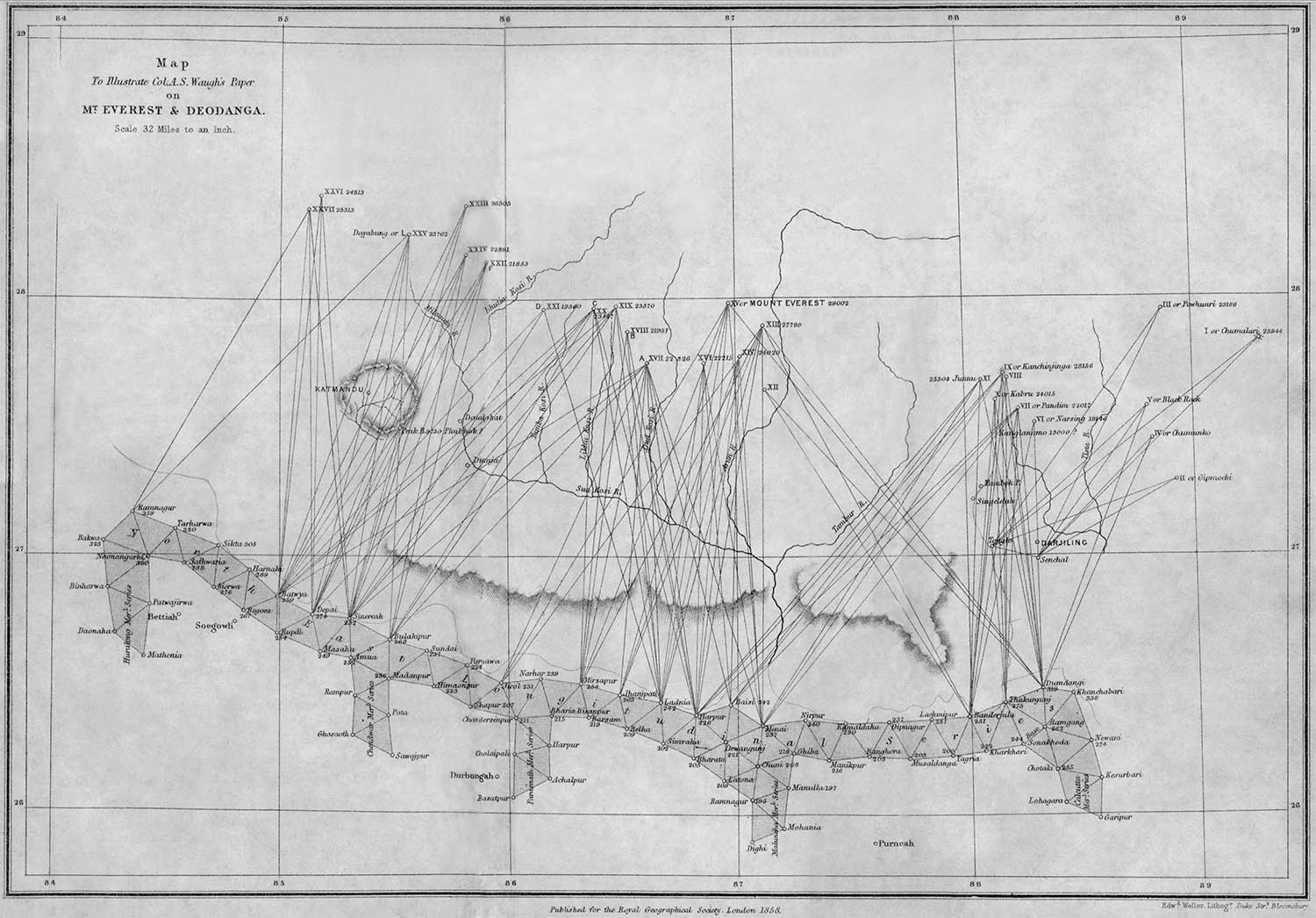
The image above comes from the excellent http://www.codex99.com/cartography/47.html... another page about the mapping of Everest. Note that is http, not https. You'll hve to copy/paste the URL to your browser. Please let me know if you find they've fixed the issues that blocked httpS accress when I tried it.
If the map doesn't take your breath away, look at it some more, and think. Completed before 1863, just for a start, teams lugged heavy, delicate equipment to 15 sites. From them made multiple very careful observations of between 2 and 14 (or more?) distant peaks. Every "observation" was only as good as the bearings to two distant points.
If it doesn't take your breath away, at least, please, concede that it is a thing of beauty?
Then the "back in the lab" work began. Breathtaking. And none of THAT possible until the chain of trig stations had been established. A much bigger task. And so far we are only taking of the lat and long of the many peaks investitgated. Read on!...
Their figure: 29,002. Today's figure: 29,029... and today's scientists have fancier techniques, and closer access available to them. Pretty remarkable, I would say. Seeing as both figures include the snowcap (11 ft, at the time of one team's measurement), the 27 foot "discrepancy" becomes even more trivial. Furthermore, the height of the underlying rock is not constant! Some calculate a change of 4mm per year upwards. If that rate has been constant (unlikely, of course), then between 1856 and 2013, the height change would eliminate two of the "disputed" 27 feet!
Let's put it another way. The difference between 29,002 and 29,029 is equivalent to an error of 5 feet in one mile. Could you measure a mile, to within five feet, over a straight bit of road with a ruler? How about measuring the height of an island volcano above the surrounding sea from another island 108 miles away? You see, I hope, what happens when you ruminate upon the achievement of the team Colonel Waugh
All of the height measurements depend, of course, on knowing where "zero" is... quite a feat in itself, but a story for another time, perhaps.
-----
An "unimportant" personal note, but I hope you will be amused by it, as I am: I've known about the wonder of the determination of Everest's height for many years. And then, very recently, I learned that a contemporary distant cousin is a Waugh... of the Everest Waugh's line!
Going back to where we started: The Great Trigonometrical Survey of India. It created a "backbone" of accurately mapped points in chains across the length and breadth of the country, the basis for an accurate map. (I discuss the process of generating such points in two different essays. If you are reading this on a Tuesday, Thursday, or Saturday, perhaps try the page couched as a challenge to programmers? I believe it contains information of general interest, and that the programming content is minimal.) If reading this on one of the other days, perhaps try the one that proposes that you try map making for yourself? (And if you are feeling really kind, then glance at the other, and send me your thoughts?)

Look at the small detail of the Survey's work between Cochin and Madras, below. I count about 200 little circles where lines meet on that. (Try just counting them.)
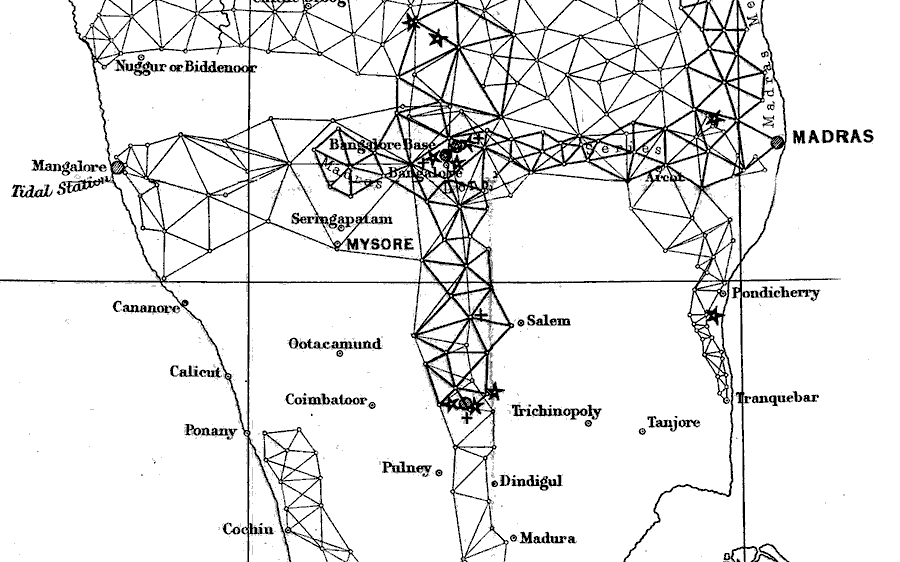
Each small circle is a place where the Survey team went, set up a theolodite, and made many readings... to see if they got the same answer each time. The lines show you what other sites the surveyors were measuring angles between from the circle you are currently considering.
Remember that this is just a small fragment of the overall project. I had a wonderful trip to India in 2007. We visited Cochin and Madras... but we used an airplane to get from one to the other. We didn't trek overland, climbing tall hills (and/ or building scaffolding towers) along the way. It is over 300 miles. And the roads, hotels and medicines in the 1800s weren't what they are today. Just visiting the trig points was an amazing achievement! Try to think about all of this in the next few days. The survey, even without the determination of Everest/ Chomolungma's height, was a stupendous accomplishment.
The main "backbone" of the skeleton is 1600 miles long. Doing the chain of triangles for just that would be pretty daunting, don't you think? Remember that you must find a sequence places where you can see at least two previously visited places, and, in fact, the surveyors would "need" more than that, at every station, in order to be able to make "extra" measurements which would act as checks on the core measurements.
I didn't show you the whole index, because you can't see the detail at that scale. It would be like trying to appreciate one neighborhood from an aerial view of all of a whole city. You can see an image of the whole index at Wikipedia's page.
I wish I could give you better images of the index to the Great Trigonometric Survey... properly rendered, it is gorgeous. There's a good one out there on the net somewhere as a huge .png... but I couldn't find it today, and I'm not sure of the copyright considerations on that one, anyway. Sigh.
There are, of course, many good sites about the survey on the web. One that caught my eye was the one Cambridge University's science magazine (https://www.srcf.ucam.org/bluesci/), but sadly, that site no longer allows deep links, so good luck finding it. What it had to say might have helped you grasp one of the things that amazed me about the survey.
Here's a bit of a map published in 1883, "Compiled from the most recent topographical and revenue surveys, based on the Great Triangulation." (It covers nearly the same part as in the illustrations above.)
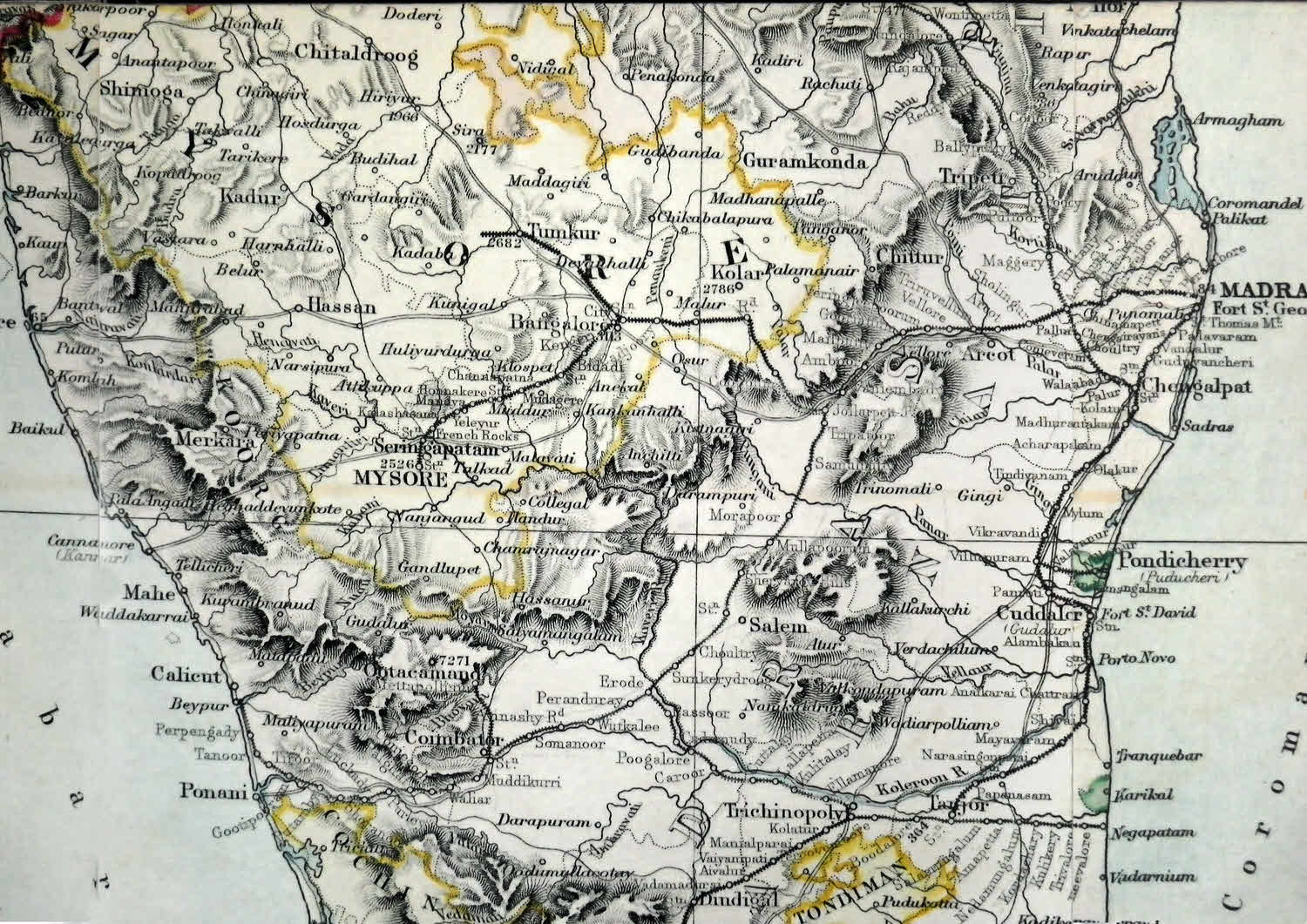
Earlier, I tried to convince you that just looking a the mountain range it isn't immediately clear which is the highest.
Perhaps this NASA photo mosaic made from photos taken in January 2004 taken from the International Space Station will help make that point. (Thank you Wikimdia Commons... have you $upported their work recently?.... And did notice the proposed attack from the EU, which could shut down large parts of what they do... and who's to say they won't come back again?)

I wonder if Everest and the rest ever dreamed of being able to use a "super balloon" one day, to get views like this?
Search across all my sites with the Google search button at the top of the page the link will take you to.
Or...
Search SheepdogGuides.com site, including Flat-Earth-Academy...
|
What's New at the Site / / Advanced search
This search tool (free to me and to you) provided by FreeFind.com... whom I've used since 2002. I'm happy with them... obviously!
Unlike the clever Google search engine, FreeFind's merely looks for the words you type, so....
* Spell them properly.
* Don't bother with "How do I get rich?" That will merely return pages with "how", "do", "I"....
Disclosure: FreeFind tells me what people have searched for. It doesn't tell me your personal details. (If someone would "spy" on you, wouldn't they also feel free to lie in a "privacy statement"? Not to say I'm not lying... how can you tell?... but to say "What are privacy statements worth?".
The search engine merely looks for the words you type, so....
*! Spell them properly !*
Don't bother with "How do I get rich?" That will merely return pages with "how", "do", "I", "get" and "rich".
I have other sites. My Google custom search button will include things from them....
One of my SheepdogGuides pages.
My site at Arunet.
This page's editor, Tom Boyd, will be pleased if you get in touch by email.
Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. It passes in some important ways, but still needs work to fully meet HTML 5 expectations.
. . . . . P a g e . . . E n d s . . . . .